Abstraction

Sometimes when we first try to solve a problem, we can get overwhelmed by the details. This makes it difficult to find a solution.

Abstraction means ignoring the irrelevant details, and concentrating on the parts of the problem or task that really matter.

Sorting your class by height

Suppose your teacher asked the class to line up in height order, with the tallest student at one end and the shortest student at the other end. There would probably be a period of confused milling around, maybe even some disagreements, and after quite a lot of swapping and changing the class would in the right order:

class

If someone asked you to describe how the class came to be in the right order, it might be quite difficult. There are so many things going on, people moving around, people of similar height trying to decide who is slightly taller, that any kind of method gets lost in the noise. To try to understand the process, we can look at a similar, but slightly different, problem.

Sorting the class by name

Now suppose you have the names of all your classmates, each written on its own bit of paper. You have been asked to sort the bits of paper in alphabetical order.

There are various ways to do this, but here is what you might do. Pick a name from the start of the alphabet, and put it on the left, pick a name from the end of the alphabet and put it on the right. Maybe pick a name from the middle of the alphabet and put it in the middle.

class names

Then, take each of the other names, one by one, and put it in the right place, in between a name which is lower and a name which is higher (in alphabetical terms). Sometimes you might need to move the bits of paper along to make space. By the time you have finished, the names will be sorted:

class names

Now you probably have a much better idea of how this process worked, because you moved all the bits of paper around yourself, rather than watching a bunch of people all doing their own thing. But sorting the names has a great deal in common with the students lining up by height.

Abstracting

You can probably see how these two activities share a lot of similarities. You are taking a set of items (students, or bits of paper) and sorting them in some way (by height, or alphabetically), then placing the result in some kind of ordered structure (a line of students, or a list of names).

In fact, once the first few students have started to form a line, what will often happen is that the remaining students will try to find their place in the line, and squeeze in. This is exactly the same as you would do with the bits of paper when sorting the students' names.

When we use abstraction, we get to the root of the problem, and the solution we find might be useful for many different situations. Sometimes we use the term "generalisation" instead of abstraction, because we are finding a general purpose solution.

Computers often need to sort items (usually numbers or strings). We often use a comparison operator such as < (less than) to sort values, and place the result in a list (or array). The method we used here is similar to an algorithm called insertion sort, but there are many other [sorting algorithms] (/algorithms/sort). Here is the essence of our sorting process for each case:

abstract sort

Abstract data - maps

We can apply abstraction to data too. This means that we concentrate on the parts of the data we need to solve our problem, and don't worry too much about the rest.

A classic example of data abstraction is a map. A map represents part of the real world, but it only tells you certain things about the world. For example, a street map will show you the roads and important buildings. But it won't show the individual houses and their numbers - that is more detail than you need just to find your way around a town. It won't usually show you whether each road is flat, or a hill.

One of the most abstract maps you will find is the iconic London Underground map. This map shows the Tube stations, and the lines which connect them.

tube

It doesn't show you anything about the world above ground. The stations aren't even in the correct places, geographically. The distance between two stations on the map does not reflect the real distance between them, most lines are straight (even though they might have bends), and in many cases the tracks aren't going in the exact direction shown on the map.

But that doesn't matter, because when you are underground all you really need to know is which line you need to take, and in which direction. The map tells you that very clearly, with minimum distractions.

Turtle graphics

We have seen previously how to draw different shapes using turtle graphics:

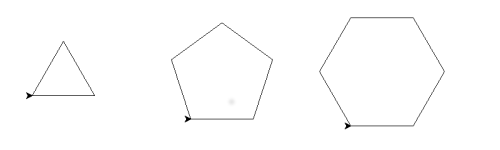
polygon

What are the essential, abstract features of each shape?

You might think that one of the features is the angle the turtle turns through at each corner. But maybe that isn't quite right - the really important thing about a polygon is how many sides it has. If you know how many sides it has, you can work out what the angle should be.

Another important feature is the size of the polygon. You might think that you can specify the length of the sides, but that isn't quite good enough. The triangle and the hexagon both have the same length sides (100 pixels) but the shapes are not the same size. A better way to specify the size of a polygon is by the radius of the circle that encloses it:

polygon

So now we know the steps involved in drawing a polygon, and we know that its abstract qualities are the number of sides and the radius of the enclosing circle, the next thing to do is create an algorithm for drawing any regular polygon with a turtle.

Abstraction

Sorting your class by height

Sorting the class by name

Abstracting

Abstract data - maps

Turtle graphics

Computational thinking

See also

Links